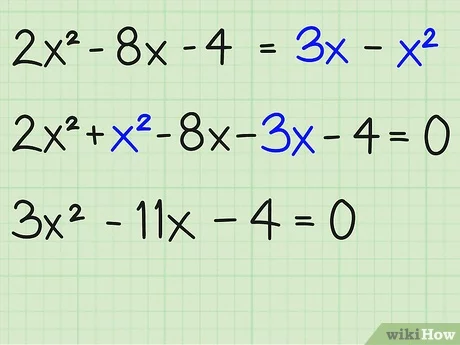චතුරස්රාකාර සමීකරණ විසඳීම

චතුරස්රාකාර සමීකරණය ගණිතමය සමීකරණයක් වන අතර, එය පොදුවේ මේ ආකාරයෙන් පෙනේ:

ax² + bx + c = 0

මෙය සංගුණක 3ක් සහිත දෙවන අනුපිළිවෙල බහුපදයකි:

• a - ජ්යෙෂ්ඨ (පළමු) සංගුණකය, 0 ට සමාන නොවිය යුතුය;
• b - සාමාන්ය (දෙවන) සංගුණකය;
• c නිදහස් අංගයකි.

චතුරස්රාකාර සමීකරණයකට විසඳුම වන්නේ සංඛ්යා දෙකක් (එහි මූලයන්) සොයා ගැනීමයි - x₁ සහ x₂.

මූලයන් ගණනය කිරීම සඳහා සූත්රය

චතුරස්රාකාර සමීකරණයක මූලයන් සොයා ගැනීම සඳහා, සූත්රය භාවිතා කරනු ලැබේ:

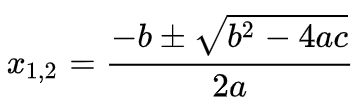
වර්ගමූලයේ ඇතුළත ප්‍රකාශනය හැඳින්වේ වෙනස් කොට සැලකීම සහ අකුරින් සලකුණු කර ඇත D (හෝ Δ):

D = b² - 4ac

මෙ මාවතින්, මූලයන් ගණනය කිරීමේ සූත්‍රය විවිධ ආකාරවලින් නිරූපණය කළ හැකිය:

1. නම් D > 0, සමීකරණයට මූලයන් 2ක් ඇත:

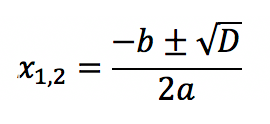
2. නම් D = 0, සමීකරණයට ඇත්තේ එක් මූලයක් පමණි:

3. නම් D < 0, вещественных корней нет, но есть комплексные:

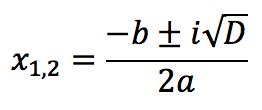
චතුරස්රාකාර සමීකරණවල විසඳුම්

උදාහරණයක් 1

3x² + 5x +2 = 0

තීරණ:

a = 3, b = 5, c = 2

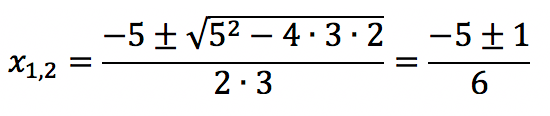
x₁ = (-5 + 1) / 6 = -4/6 = -2/3

x₂ = (-5 – 1) / 6 = -6/6 = -1

උදාහරණයක් 2

3x² - 6x +3 = 0

තීරණ:

a = 3, b = -6, c = 3

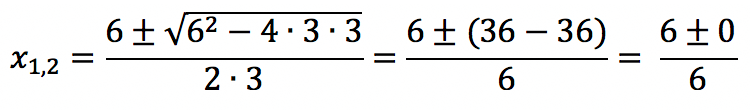
x₁ = x₂ = 1

උදාහරණයක් 3

x² + 2x +5 = 0

තීරණ:

a = 1, b = 2, c = 5

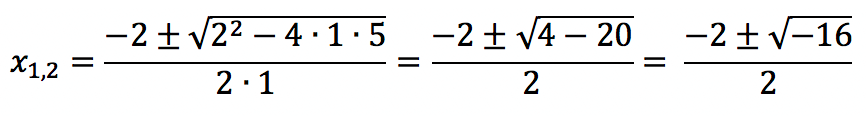
මෙම අවස්ථාවේ දී, සැබෑ මූලයන් නොමැති අතර, විසඳුම සංකීර්ණ සංඛ්යා වේ:

x₁ = -1 + 2i

x₂ = -1 - 2i

චතුරස්රාකාර ශ්රිතයක ප්රස්ථාරය

චතුරස්රාකාර ශ්රිතයේ ප්රස්ථාරය වේ උපමාවක්.

f(x) = ax² + bx + සී

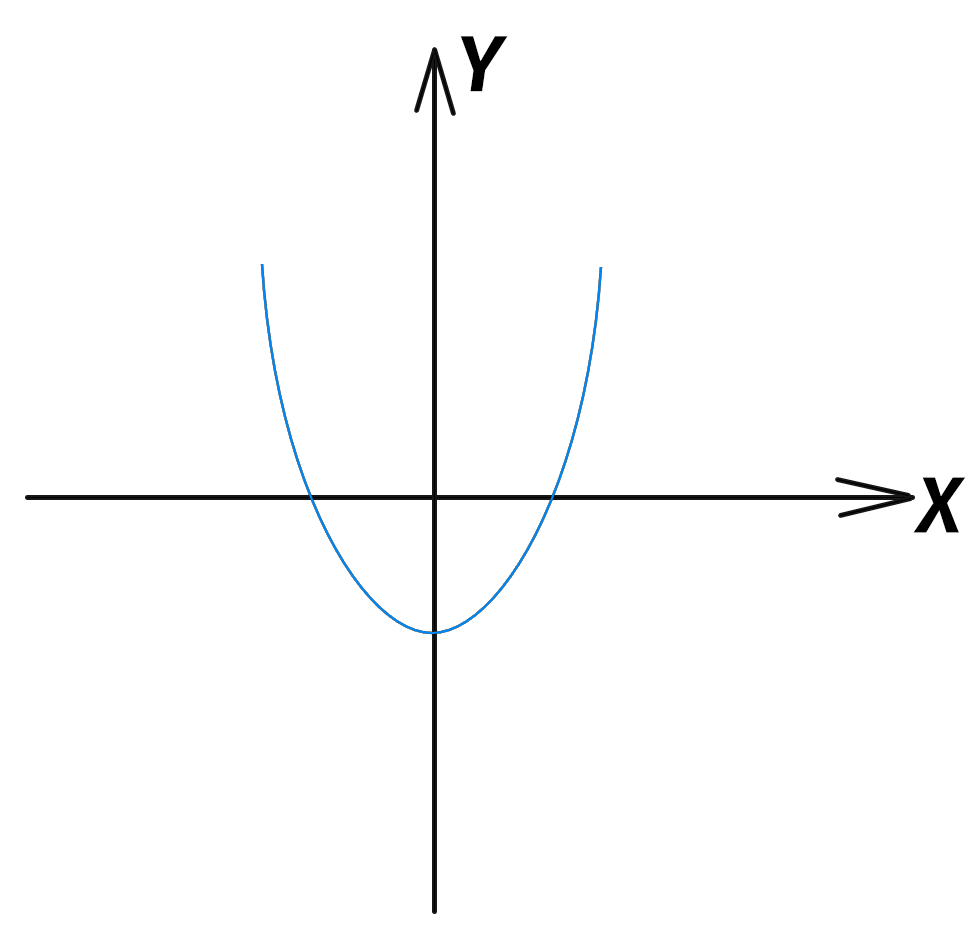
• චතුරස්රාකාර සමීකරණයක මූලයන් යනු abscissa අක්ෂය සමඟ පරාවලය ඡේදනය වන ස්ථාන වේ. (X).
• එක් මූලයක් පමණක් තිබේ නම්, පරාවලය අක්ෂය හරස් නොකර එක් ස්ථානයක ස්පර්ශ කරයි.
• සැබෑ මූලයන් නොමැති විට (සංකීර්ණ ඒවා තිබීම), අක්ෂයක් සහිත ප්‍රස්ථාරයක් X ස්පර්ශ නොකරයි.